10 - MPM2D - General Math

EXAM REVIEW

JSON REVIEW

• Length of line segment $distance=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$
• Quad formula $zeros=\frac{-b\pm \sqrt{b^2-4ac}}{2(a)}$
• slope point form
• calculating medians
• DECAY IS $a{b}^x$
  • a = Initial
  • b = rate of decrease
  • x = n cycles
• Herons $$\begin{gathered} \text{displaylines}S=(AB+BC+CA)/2 \\ Area=S(S-AB)(S-BC)(S-CA) \end{gathered}$$
• Quadratic forms
  • Completing a square is $ax+bx+c$ - You can find C by $(b/2{)}^2$ and complete it via $\sqrt{c}$ or $b/2$
  • factored form conversions
  • CALCULATING THE LENGTH OF A LINE SEGEMENT
  • PERP BISECTORS

Slopes

Perpendicular slopes are the negative reciprocal

• e.g. m = 2/5 & 5/-2 are perpendicular

Trig

Calculating shortest distance

Flip opposing line’s slope then do algabra ,

:::spoiler 02-29
ABC has vertices A(3,4), B(-5,2) and C(1,-4)
a) an equasion for CD the median from C to AB

D = midpoint of AB
D = (-1, 3)

Slope of CD = -7/2

so then y = (-7/2)x + b
sub D into that so
3 = (-7/2)(-1) + b
3-(-7/2) = b
6.5 = b
so finally y = -7/2 + 6.5

b) an equation for GH the right bisector of AB

M(ab) = 4-2/3-(-5) = 2/8 = 1/4

perpendicular bisector of that is -4 since you swap it to 4/1 then * -1

so now
y = -4x + b

sub in the midpoint which is -1,3
3 = -4(-1) + b

3 - 4 = b
b = -1

y = -4x + -1

c) an equation for CE, the altitude from C to AB

C = 1,-4

$y=mx+b$

M(ab) = 1/4
alternate is -4

$y=-4x+b$

line passes through C

$-4=-4(1)+b$

$y=-4x$

# [ch7] unit 6 :: trig w/ right triangles

similar triangles and solving problems with similar triangles (c7.1, c7.2)

• congruent figures have the same size and shape

• similar figures have the same shape but different sizes

  • these can be rotated, scaled, and (reflected?)

  • they have the following properties

    1. correspdonging angles are equal
       • $\angle A=\angle T$ ;; $\angle B=\angle U$ ;; $\angle C=\angle V$
    2. ratios of corresponding sides are equal
       • $\frac{AB}{TU}=\frac{BC}{UV}=\frac{CA}{VT}$ ;; $AB:TU=BU:UV=CA:VT$
    3. the scale factor $k$ relates the lengths of corresponding sides of similar figures
       • $\frac{AB}{TU}=\frac{BC}{UV}=\frac{CA}{VT}=k$
       • the square of the scale factor relates the areas of two similar figures
         • $\frac{A_{△\text{ABC}}}{A_{△\text{TUV}}}=k^2$ ;; $A_{△\text{ABC}}=k^2(A_{△\text{TUV}})$

• naming triangles

  • all angles are capitals
  • all sides are lowercase
  • the angle opposite/across from it should be the same letter but lower case

• the symbol ~ is used to indicate similarity

• angle properties:

  1. opposite angles :: when two line intersect, opposite angles are equal
  2. supplementary angles :: angles that sum up to $180°$
  3. complementary angles :: angles that sum up to $90°$
  4. alternate angles :: z-pattern [when a transversal crosses parallel lines]
  5. corresponding angles :: f-pattern [when a transversal crosses parallel lines]
  6. co-interior angles :: c-pattern [when a transversal crosses parallel lines]
  7. the angles opposite the equal sides of an isosceles triangle are equal
  8. the sum of interior angles in a triangle is $180°$

the tangent ratio (c7.3)

• tangent of a ratio → ratio fo the side opposite an angle to the side adjacent to the angle
  • $\tan \theta =\frac{\text{opposite}}{\text{adjacent}}$

• u can use a scientific or graphing calcualtor to
  - express the tnagnent of an agnle as a decimal
  - find on eof the acute angles when both leg lenghts are knwon in a right trianlge
  - find a side length if one acute angle and one leg of a right triangle are knwon

  • ex1:
    $\tan 40°=0.8390996312\doteq 0.8$

  • tangent and inverse tangent (aka arctan) are opposite operations, like addition and subtraction

  • ex1:

    A=\tan^{-1}(1.782) \\, A=60.70028759\degree \doteq61\degree$$ "The inverse tangent of 1.782 is approximately equal to 61 degrees."

  • ex2:
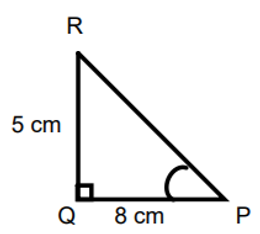
    In $△PQR$ find $\tan P$ and $\angle P$ to the nearest tenth and degree.
    
    $\tan P=\frac{5}{8}=0.625\doteq 0.6$
    $\angle P={\tan }^{-1}(\frac{5}{8})\doteq 32°$

  • ex3:
    find $x$

    $\tan x=\frac{20}{40}=\frac{1}{2}$
    $x={\tan }^{-1}(\frac{1}{2})=60°$

sine ratio and cosine ratio (c7.4)

• $\sin \theta =\frac{\text{opposite}}{\text{hypotenuse}}$
• $\cos \theta =\frac{\text{adjacent}}{\text{hypotenuse}}$
• SOHCAHTOA
  • sine equals opposite over hypotenuse ;; cosine equals adjacent over hypotenuse ;; tangent equals opposite over adjacent
  • $\sin \theta =\frac{\text{opposite}}{\text{hypotenuse}}$ ;; $\cos \theta =\frac{\text{adjacent}}{\text{hypotenuse}}$ ;; $\tan \theta =\frac{\text{opposite}}{\text{adjacent}}$
  • used to find:
    • an angle given two side lengths
    • to find one side length given an angle and one of the acute angles
• ex:
  • $\sin 75°=0.966$
  • $\cos 36°=0.809$
  • $\sin q=\frac{8}{17}$
    $q={\sin }^{-1}(\frac{8}{17})=28.07°$
• ex:
  a ladder is leaning against a wall at a $60°$angle. the height from the ground to the top of the ladder is 3m. what is the length of the ladder to the nearest tenth of a meter?

soh ! (of sohcahtoa)
$\sin 60°=\frac{3}{l}$
$l=\frac{3}{\sin 60}=2\sqrt{3}\doteq 3.5$

solving problems in triangles (c7.5)

• angle of depression :: the angle measured downward between the horizonal and the line of sight from the observer to an object

• angle of elevation :: the angle measured upward between the horizonal and the line of sight from the observer to an object

• ex1:
  from a boat on the water the angle of elevatoin of the top of a cliff is $31°$. From a point $300$m closer to the cliff, the angle of elevation is $33°$. find the height of the cliff.

  $\tan 33°=\frac{h}{x}$
  $\tan 31°=\frac{h}{300+x}$
  $x=\frac{h}{\tan 33}$
  $x=\frac{h}{\tan 31}-300$
  $\frac{h}{\tan 33}=\frac{h}{\tan 31}-300$
  $\frac{h}{\tan 33}-\frac{h}{\tan 31}=-300$
  $h(\frac{1}{\tan 33}-\frac{1}{\tan 31})=-300$
  $h=\frac{-300}{\frac{1}{\tan 33}-\frac{1}{\tan 31}}$
  $h=2411.294144\doteq 2411$

• ex2:
  kim and yuri live in apartment buildings that are $30$m apart. the angle of depression from kim’s balcony to where yuri’s building meets the ground is $40°$. the angle of elevation from kim’s balcony to yuri’s balcony is $20°$. how high is yuri’s balcony and how high is kim’s balcony?

  $\tan 40=\frac{k}{30}\to k=25.2$
  $\tan 20=\frac{y-k}{30}\to y-k=10.9$

  $y=10.9+25.2=\boxed{36.1}$