Jason Cameron

2025-02-07

2 min read

pg 38 1-3 (pg 28 tectbook)

1

---
title: Graph 1 
xLabel: 
yLabel: 
bounds: [-10,10,-10,10]
disableZoom: false
grid: true
---
f(x) = x
g(x) = 1/x
F(x)
  • straight line that passes through 0,0
  • has a slope of 1
  • extends forever in both directions
G(x)
  • Curved equation with two branches.
  • The function is undefined when x=0 so there is a asymptote.

Similarities

  • Both pass through -1, -1 and 1,1
  • Both are symetrical around their origin

Differences

  • f(x) is a straight linear line
    • g(x) is a curve
  • f(x) passes through all points on it’s graph
    • g(x) cannot pass where x=0 or y=0

The equations of the asymptotes for are:

  1. Vertical asymptote:
  2. Horizontal asymptote:

2

---
title: Graph 2
xLabel: 
yLabel: 
bounds: [-10,10,-10,10]
disableZoom: false
grid: true
---
f(x) = x^2
g(l) = abs(l)

These graphs are alike as they are both symetrical and are valid functions, they also both have curves and when scaled very far out appear to be on the axis.

These graphs are different as x^2 is continuous and is one (infinite) line. 1/x is not continuous and has two distinct parts due to the asymptote.

---
title: 
xLabel: 
yLabel: 
bounds: [-10,10,-10,10]
disableZoom: false
grid: true
---
h(x) = x
g(x) = sqrt(x)
f\left(x\right)\ =\ \frac{1}{x}\left\{x\ge0\right\}

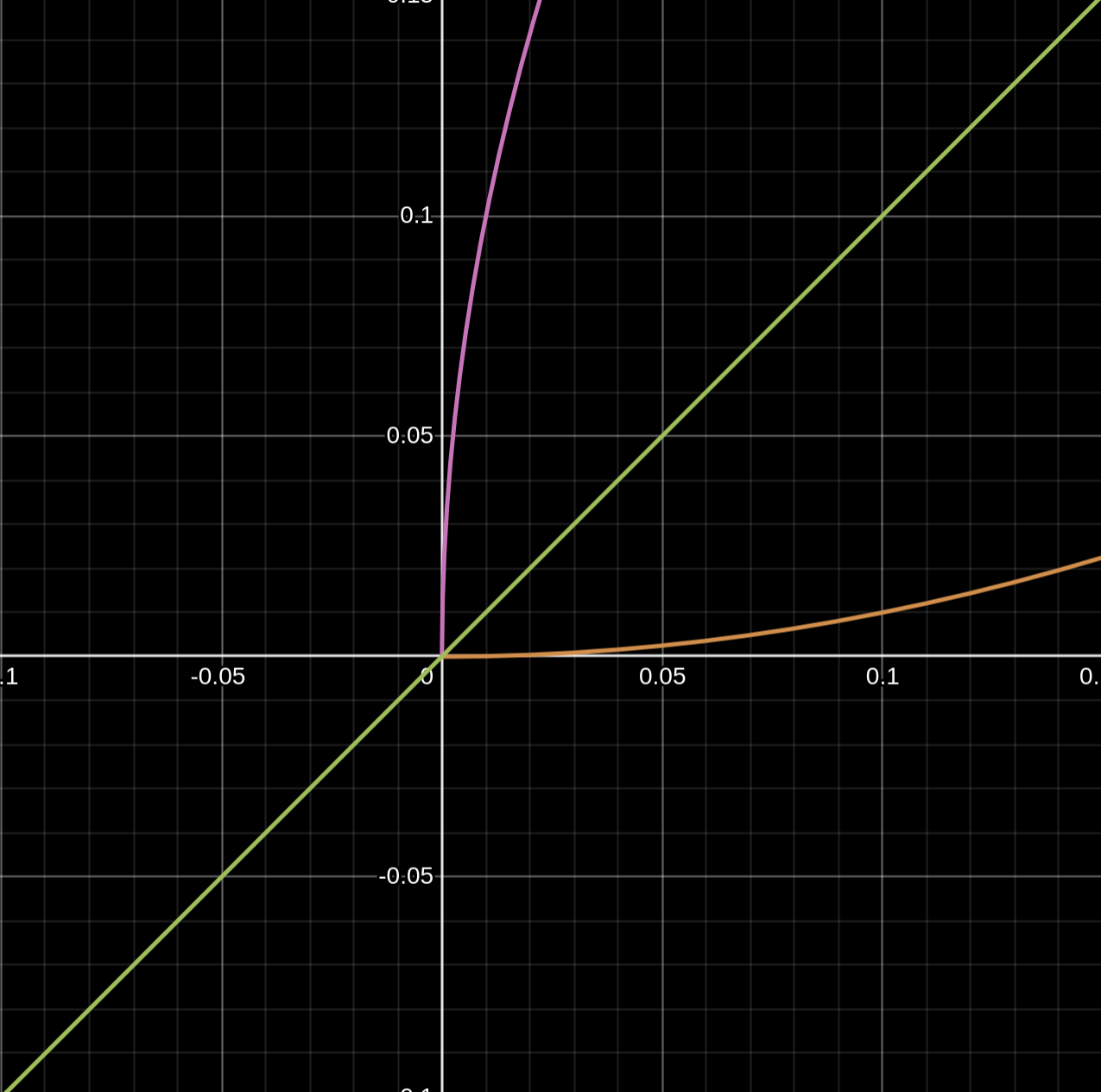
All three of these graphs are related. They also take in X as an imput and are valid functions.
sqrt(x) is the inverse of x^2 while x goes thorugh the center.

Graph View